TD 6 7 8 : Programmation
linéaire
Exercice 1 :
Dans un établissement, un groupe d’étudiants se charge de
l’approvisionnement en pains au chocolat et en croissants de machines
automatiques.
Lors d’une période donnée dans la journée ils ont constaté que pour pouvoir
satisfaire la demande, ils doivent disposer au minimum de 36 pains au chocolat
et de 24 croissants.
Deux boulangers proposent pour le même prix de 3€.
- l’un le lot A comprenant 4 pains au chocolat et 2 croissants ;
- l’autre le lot B composé de 3 pains au chocolat et 3 croissants.
On souhaite déterminer le nombre de lots A et le nombre de lots B qui doivent être achetés pour satisfaire la demande au moindre coût.
Ecrire le programme linéaire formalisant ce problème et le résoudre graphiquement.
Exercice 2 :
Une machine M permet de fabriquer deux types de
produits P et Q mais ces deux types ne peuvent être produits simultanément. M
est disponible 100 heures par semaine. 30 unités de P ou 50 unités de Q peuvent
être produites à l'heure. Chaque unité de P et chaque unité de Q laissent
respectivement un revenu net de 10u.m. et de 30u.m. Les demandes sont telles
que l'on ne doit pas produire plus de 2 000 unités de P ni plus de 4 000 unités
de Q par semaine.
Déterminer graphiquement puis par la méthode du
simplexe les quantités de P et Q à produire par semaine pour rendre le revenu
net total maximum.
Exercice 3 :
On considère le programme linéaire suivant à résoudre par la méthode du simplexe
Max 3X + 5Y + 4Z
2X +2Y +2Z <= 420
X + 2Y + 3Z <= 360
Exercice 4:
Une entreprise extrait un minerai dont elle tire
deux composants A et B.
Elle possède 3 mines. A partir d’un mètre cube
extrait on obtient selon la mine les résultats suivants:
|
|
Quantité de A en tonnes |
Quantité de B en tonnes |
|
Mine 1 |
2 |
2 |
|
Mine 2 |
2 |
1 |
|
Mine 3 |
1 |
2 |
Les coûts d’extraction d’un mètre cube sont
respectivement de 50u.m. pour la mine1
30u.m. pour la mine 2 et 40u.m. pour la mine
3.(u.m. unités monétaires)
On veut
produire à moindre coût 250 tonnes de A et 200 tonnes de B.
1) Formaliser le problème sous forme d'un
programme linéaire mis sous forme standard.
2) On se propose d’extraire 75 mètres cubes de
la mine 1; 50 de la mine 2, la mine 3
restant inexploitée. Montrer que ce plan est réalisable et correspond à une
solution de base.
3) Après avoir mis le problème sous forme
canonique par rapport à la base précédente poursuivre l’algorithme du simplexe
jusqu’à l’optimum.
4) Ecrire le programme dual et déduire son
optimum de celui du primal.
Dans le cadre d’une campagne promotionnelle, la société RicaPizza décide de consacrer une partie de ses ressources à la confection de parts de pizza vendues avec de faibles marges.
Elle décide de proposer les types de pizza suivants : Margarita, Reine, et Napolitaine.
L’entreprise décide de consacrer à cette campagne les ingrédients suivants conditionnés par doses et disponibles dans les quantités suivantes:
Ingrédients |
Nombre de doses disponibles |
|
Coulis de tomates |
9600 |
|
Mozarelle |
6000 |
|
Olives |
2500 |
|
Jambon |
450 |
|
Anchois |
250 |
|
Champignons |
400 |
Ramenées à une part le nombre de doses d’ingrédients nécessaires est précisé ci-dessous :
|
|
Margarita |
Reine |
Napolitaine |
|
Tomates |
8 |
5 |
6 |
|
Mozzarelle |
5 |
3 |
4 |
|
0lives |
2 |
1 |
2 |
|
Jambon |
0 |
1 |
0 |
|
Anchois |
0 |
0 |
1 |
|
Champignons |
0 |
1 |
0 |
Enfin le bénéfice escompté par part de pizza vendue est de 10 centimes pour la Margarita, 20 centimes pour le Reine et 15 centimes pour la Napolitaine.
1) Ecrire le programme linéaire permettant de déterminer le bénéfice maximum. (On écrira les contraintes dans l’ordre des ingrédients du tableau ci-dessus).
2) Ecrire le problème sous forme standard.
3) Après avoir écrit le tableau du simplexe correspondant, effectuer la première itération.
4) Après un certain nombre d’itérations on obtient le tableau suivant :
|
Base |
X1 |
x2 |
x3 |
e1 |
e2 |
e3 |
e4 |
e5 |
e6 |
sgm |
|
e1 |
0 |
0 |
0 |
1 |
-1.6 |
0 |
0 |
0.4 |
-0.2 |
20 |
|
x1 |
1 |
0 |
0 |
0 |
0.2 |
0 |
0 |
-0.8 |
-0.6 |
760 |
|
e3 |
0 |
0 |
0 |
0 |
-0.4 |
1 |
0 |
-0.4 |
0.2 |
80 |
|
e4 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
-1 |
50 |
|
x3 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
250 |
|
x2 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
400 |
|
feco |
0 |
0 |
0 |
0 |
-2 |
0 |
0 |
-7 |
-14 |
-19350 |
a) Quelle est la production optimale et le bénéfice correspondant ?
b) Quels sont les ingrédients totalement utilisés ?
c) Que devient la production optimale et le bénéfice correspondant si l’on dispose de 10 doses supplémentaires de mozzarelle ?
Exercice 6 :
Dans une entreprise E on fabrique des produits
P1, P2, P3 à l'aide de 3 matières premières M1, M2, M3 dont les stocks sont
respectivement de 130, 200, et 140 unités.
Les processus de fabrication respectifs ont les
caractéristiques techniques suivantes:
Pour fabriquer une
unité de P1, on utilise 2 unités de M1, 1 de M2 et 1 de M3.
Pour fabriquer une
unité de P2, on utilise 2 unité de M1, 2 de M2 et 2 de M3.
Pour fabriquer une
unité de P3, on utilise 1 unité de M1, 2 de M2 et 1 de M3.
Les bénéfices unitaires réalisés par la vente de
chaque produit sont de 12 pour P1, 15 pour P2 et 10 pour P3.
1) Ecrire
le programme linéaire de production (sous sa forme standard) de l'entreprise E.
2) Trouver
la solution optimale en utilisant la méthode des tableaux du simplexe.
3) Quelle
est la base optimale?
4) On
considère le tableau suivant:
|
base |
x1 |
x2 |
x3 |
e1 |
e2 |
e3 |
sgm |
|
|
1.5 |
1 |
0 |
1 |
-0.5 |
0 |
30 |
|
|
-1 |
0 |
1 |
-1 |
1 |
0 |
70 |
|
|
-1 |
0 |
0 |
-1 |
0 |
1 |
-10 |
|
feco |
-0.5 |
0 |
0 |
-5 |
-2.5 |
0 |
-1150 |
a) Que peut-on en dire ? (A-t-on une forme
canonique ? Si oui par rapport à quelle base, cette base est-elle réalisable ?
etc..).
b) Peut-on appliquer l'algorithme dual pour
trouver la solution optimale? Pourquoi ?
c) Si oui appliquer cet algorithme (Indiquer la
variable entrante la variable sortante et effectuer le pivot).
5) On reprend le tableau trouvé question 2). Que devient ce tableau si on indique que le stock de la ressource M3 n'est plus de 140 mais de 120 ? En déduire la solution optimale du problème initial dans ce cas.
Exercice 7:
Une usine chimique
peut produire 3 variétés de matières synthétiques par mélange de 3 composants
A, B et C. Les données techniques de
la production sont les suivantes:
Pour produire 1 kg de la variété V1, il faut 2 kg de A, 2 kg de B et 1
kg de C
Pour produire 1 kg de la variété V2, il faut 1 kg de A, 2 kg de B et 1
kg de C
Pour produire 1 kg de la variété V3, il faut 1 kg de A, 2 kg de B et 2
kg de C
L'usine dispose de
400 kg de A, de 500 kg de B et de 400
kg de C par jour.
Les variétés V1, V2 et V3 sont vendues avec
des marges bénéficiaires unitaires respectives de 5 €, 3 € et 4€
1)
L'usine
cherche à maximiser son bénéfice quotidien. Formuler le problème en termes de
programmation linéaire en précisant la signification des variables et
contraintes.
2)
Le problème
traité avec le solveur d’excel conduit aux résultats suivants : voir
annexe ;Reconstituer au maximum possible le tableau optimal.
3)
Répondre aux
questions suivantes
a)
Quelle est la
production optimale et le bénéfice correspondant ?
b)
Quelles sont
les composants entièrement utilisés ?
c)
Pour quelle
valeur minimale de sa marge unitaire V2 serait-elle produite ?
d)
Dans quelle
fourchette doit se trouver la marge sur V1 pour avoir la même production
optimale ?
e)
Si la quantité
de composant A augmente de 10 kg quel est l’impact sur la production optimale
et sur le bénéfice ?
4) On donne le résultat suivant :
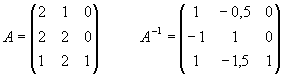
Utiliser ce résultat pour compléter le tableau optimal
5) Que se passe-t-il si le nombre de composants C n’est plus que de 300 ?
Modifier le tableau précédent pour répondre à la question posée en utilisant l’algorithme dual du simplexe
Annexe
|
Cellule
cible (Max) |
|
|
|
|
|||
|
|
Cellule |
Nom |
Valeur initiale |
Valeur finale |
|
|
|
|
|
$D$7 |
|
12 |
1150 |
|
|
|
|
Cellules
variables |
|
|
|
|
|||
|
|
Cellule |
Nom |
Valeur initiale |
Valeur finale |
|
|
|
|
|
$A$2 |
V1 |
1 |
150 |
|
|
|
|
|
$B$2 |
V2 |
1 |
0 |
|
|
|
|
|
$C$2 |
V3 |
1 |
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Contraintes |
|
|
|
|
|
||
|
|
Cellule |
Nom |
Valeur |
Formule |
État |
Marge |
|
|
|
$D$4 |
|
400 |
$D$4<=$F$4 |
Lié |
0 |
|
|
|
$D$5 |
|
500 |
$D$5<=$F$5 |
Lié |
0 |
|
|
|
$D$6 |
|
350 |
$D$6<=$F$6 |
Non lié |
50 |
|
|
Cellules
variables |
|
|
|
|
|
|||
|
|
|
|
Finale |
Réduit |
Objectif |
Admissible |
Admissible |
|
|
|
Cellule |
Nom |
Valeur |
Coût |
Coefficient |
Augmentation |
Réduction |
|
|
|
$A$2 |
V1 |
150 |
0 |
5 |
3 |
1 |
|
|
|
$B$2 |
V2 |
0 |
-1 |
3 |
1 |
1E+30 |
|
|
|
$C$2 |
V3 |
100 |
0 |
4 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Contraintes |
|
|
|
|
|
|
||
|
|
|
|
Finale |
Ombre |
Contrainte |
Admissible |
Admissible |
|
|
|
Cellule |
Nom |
Valeur |
Coût |
à droite |
Augmentation |
Réduction |
|
|
|
$D$4 |
|
400 |
1 |
400 |
100 |
50 |
|
|
|
$D$5 |
|
500 |
1,5 |
500 |
33,33333333 |
100 |
|
|
|
$D$6 |
|
350 |
0 |
400 |
1E+30 |
50 |
|